Resumen:
Uso de la Transformada Rápida de Fourier (FFT), en Osciloscopios de gama media para la descomposición de una onda cuadrada. Comparación con el cálculo matemático y precisión.
Abstract:
Use of the Fast Fourier Transform (FFT), in mid-range oscilloscopes for decoding a square wave. Comparison with the mathematical calculation and precision.
Introducción
Los osciloscopios presentan, de forma habitual, variaciones de voltaje frente a tiempo. Hay algún caso en el que la representación en pantalla es diferente, por ejemplo, en la transformada rápida de Fourier, en donde se representa la intensidad de la señal en dB o su conversión a voltaje, frente a la frecuencia. Esto da lugar a una serie de picos o armónicos de la señal así representada,para ciertos tipos de señales.
Clásicamente, se han empleado ``Analizadores de Espectros'', para analizar la amplitud de señales complejas en el espectro de las frecuencias, estos analizadores de espectros pueden servir para para estudiar Interferencias Electromagnéticas (EMI) de señales producidas por el funcionamientos de los distintos elementos de un circuito electrónico, y eliminar en el diseño estas.
Con el advenimiento de los osciloscopios digitales, parte de las funciones de los analizadores de espectros han sido tomadas por estos, salvando la distancias. Pero el objetivo de este artículo no consiste en el análisis del uso de la FFT, sino en la interpretación matemática de los resultados obtenidos, la validez de los mismos y su precisión.
¿Qué es la transformada discreta de Fourier desde el punto de vista matemático?
Cualquier función periódica, puede descomponerse en una suma de términos, seno y coseno, con un peso determinado, el ajuste de esta aproximación será tanto mejor, cuanto mayor número de términos sean usados.
Con esto cabría preguntarse si es posible representar una señal de onda cuadrada, que todos conocemos, con sus saltos abruptos, por una suma de términos de la función seno, evidentemente mas suave.
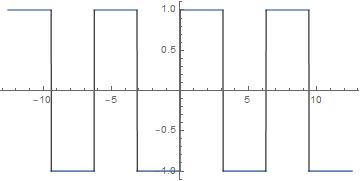
Esta es la representación de una onda cuadrada de amplitud 1.
Si definimos $A=1$ como la amplitud de la onda, el desarrollo por Fourier de la función onda cuadrada será (Ecuación 1):
\begin{equation}
\frac{(4 A) \sum _{n=1}^{\infty } \frac{\sin ((2 n-1) x)}{2 n-1}}{\pi }
\end{equation}
Vamos a representar este desarrollo con un número muy elevado de términos, pongamos 10000, vemos que con un número suficientemente elevado en el desarrollo por Fourier, prácticamente obtenemos una curva de onda cuadrada perfecta:
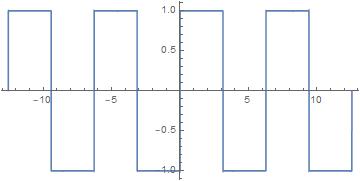
Veamos ahora como queda la misma representación con sólo 7 términos que es los que vamos a obtener con la función FFT del osciloscopio:
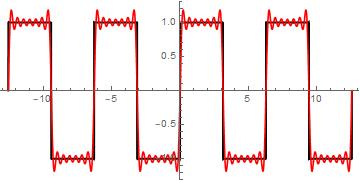
En esta última gráfica se representan simultáneamente la serie con 7 (rojo) y con 10000 términos (negro), evidentemente al bajar el número de términos la función pierde su ajuste a la función teórica, pero todavía puede considerarse aceptable.
Aplicación de la FFT generada por un osciloscopio y su comparación con el modelo matemático.
Para este experimento se han empleado dos señales de onda cuadrada de 1 MHz y de 1 KHz de frecuencia y de 1 Voltio de amplitud, para la señal de onda se ha utilizado un generador de onda: FeelElec FY 6800 y un Osciloscopio Hantek DSO5202P.
El procedimiento es el siguiente:
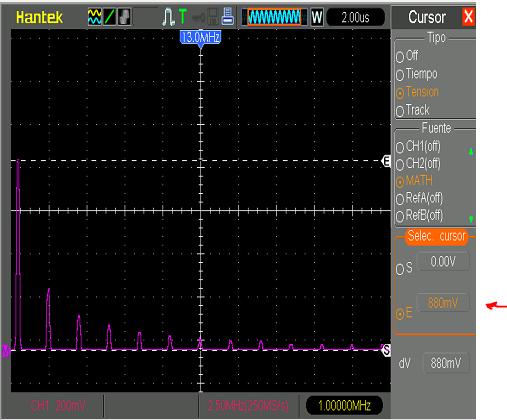
- Se introduce una señal de 1 MHz y 1 voltio de amplitud por el canal 1 del osciloscopio, como se muestra en la figura:
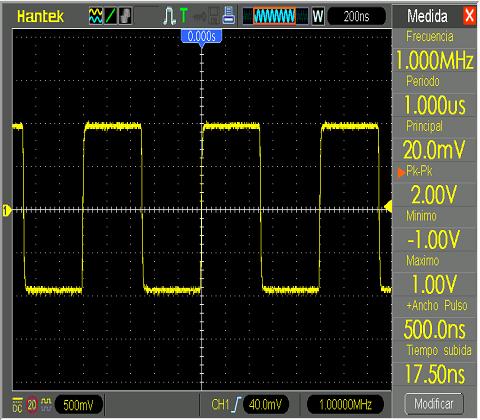
Se utiliza la función matemática FFT:
- Ventana Flattop
- FFT zoom x2
- Base vertical Vms
Los resultados se muestran en la siguiente tabla para 1 MHz 1V:
| 1 MHz | 896 mV |
| 3 MHz | 300 mV |
| 5 MHz | 182 mV |
| 7 MHz | 120 mV |
| 9 MHz | 100 mV |
| 11 MHz | 80 mV |
| 13 MHz | 60 mV |
| 1 KHz | 896 mV |
| 3 KHz | 300 mV |
| 5 KHz | 184 mV |
| 7 KHz | 120 mV |
| 9 KHz | 81 mV |
| 11 KHz | 60 mV |
| 13 KHz | 60 mV |
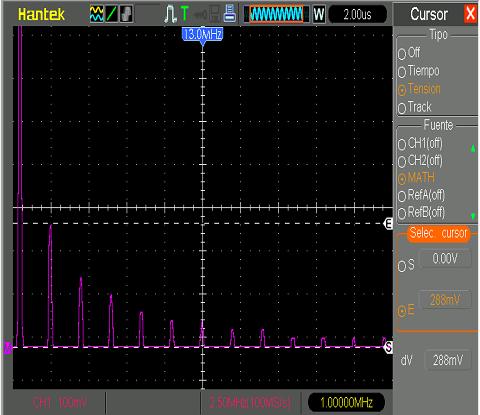 Onda cuadrada de 1KHz de frecuencia y 1 voltio de amplitud. Aplicación de la función FFT
Onda cuadrada de 1KHz de frecuencia y 1 voltio de amplitud. Aplicación de la función FFT
Se ha hecho una pequeña corrección en el generador de onda, ya que si en este se marcaba una amplitud de señal de 2 voltios pico a pico, en el osciloscopio se observaba una atenuación de aproximadamente 0.2-0.3 V, es por esto que se amplio la intensidad de la señal en el generador de onda a 2.09 para 1 MHz y 2.11 para 1 KHz, de manera que se refleja en el osciloscopio una amplitud de señal de 2 voltios pico a pico, en cada caso.
Se hacen ampliaciones de la imagen y se mide con el cursor E, la intensidad de la señal en mV, como se puede ver en las figuras, operándose de forma análoga para cada armónico, se tiene la segunda tabla..
Representemos gráficamente los resultados obtenidos, podemos optar por usar dos programas Mathematica® u Octave:
En Mathematica® creemos estas tres funciones: teórica con 7 elementos, teórica con 1000 elementos de la serie y la real obtenida con el osciloscopio, para HANTEK DSO5202 1 KHz señal cuadrada 2 v :
\begin{equation}\pmb{f[\text{x$\_$}]\text{:=}N\left[(4/\text{Pi})\sum _{n=1}^7 \frac{\text{Sin}[(2n-1)*x]}{(2n-1)},4\right]}\\\end{equation}\begin{equation}\pmb{g[\text{x$\_$}]\text{:=}N\left[(4/\text{Pi})\sum _{n=1}^{1000} \frac{\text{Sin}[(2n-1)*x]}{(2n-1)},4\right]}\\\end{equation}\begin{equation}\pmb{h[\text{x$\_$}]\text{:=}(4/\text{Pi})(0.896 \text{Sin}[x]+0.280 \text{Sin}[3x]+0.154 \text{Sin}[5x]+ 0.116 \text{Sin}[7x]+0.097 \text{Sin}[9x]+0.081 \text{Sin}[11x]+0.064 \text{Sin}[13x])}\end{equation}
Después grafiquémoslas con los siguientes comandos:
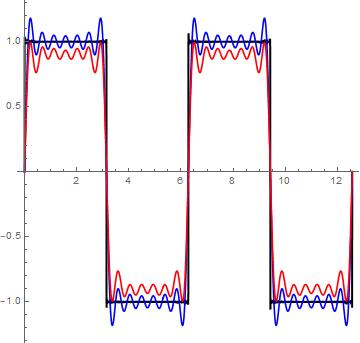
\begin{equation}\pmb{\text{Plot}[\{g[x],f[x],h[x]\},\{x,0,4 \text{Pi}\},\text{AspectRatio}\to 1,\text{PlotLegends}\to \text{{``}Expressions{''}},\text{PlotStyle}\to \{\{\text{Black},\text{Thick}\},\text{Blue},\text{Red}\}]}\\\pmb{}\\\end{equation}
Y la función corregida con el factor 1.1:
\begin{equation}\pmb{\text{Plot}[\{g[x],f[x],1.1* h[x]\},\{x,0,4 \text{Pi}\},\text{AspectRatio}\to 1,\text{PlotLegends}\to \text{{``}Expressions{''}},\text{PlotStyle}\to \{\{\text{Black},\text{Thick}\},\text{Blue},\text{Red}\}]}\end{equation}
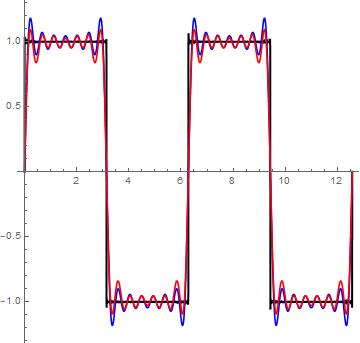
De igual forma se procede con la serie a 1KHz, obteniéndose resultados análogos.
CONCLUSIÓN:
La utilización de osciloscopios de coste medio para evaluar las FFT, da lugar a resultados satisfactorios cuasi cuantitativos y en todo caso sirven para demostrar una evaluación correcta de las transformadas rápidas de Fourier en estos equipos.
